The goal of this project is making an IC that implemented the elliptic curve cryptosystem algorithm.
ECC is a cryptography with asymetric algorithm or it’s known as public key cryptography. The security of ECC depends on the Elliptic Curve Discrete Logarithm Problem. Cryptosystem can provide high performance with this elliptic curve. It also gives better security level , smaller key size, wider bandwith, and better efficiency. An implementation of elliptic curve cryptosystem needs a high performance finite field arithmetic module.
Cryptography learn the method for sending messages in code so that only the right person can receive that. The messages which is sent called plaintext and the code messages called chipertext. The process to convert plaintext to chippertext is called encription and the reverse is called decription. According to the used key, Cryptography is divided into two parts: cryptography with private key and cryptography with public key.
Private key method provide encription process with only one key, the messages then the messages convert into codes. The codes then decript by same key into first messages, The security of this system is lied on the key. This system is also known as symetric key cryptography.
Public key crptography is done by two keys, one private key and one public key, that are related. Public key is published so that can be used for encription process. Private key only known by the owner and it is unique. The messages then encripted by public key into codes, the codes then decrited into first messages. The security of this methods is lied on mathematical power that makes no one knows private key by knowing public key. It is also called as asymetric key cryptography.
Elliptic curve equation came from Weierstrass equation. This equation is:
Y^2 +a1XY+a3Y = X^3+a2X^2+a4X+a6 (I)
Elliptic curve equation that is used on this system is equation with the character is not equal to 2 and 3 (char(K)¹2,3) so that the equation can be simplified into:
Y^2=X^3 +aX+b (2)
In elliptic curve there are three operation including addition, doubling, and scalar multiplication. Addition of two points is defined as line section which make connection between two points and the curve and then reflected to x-coordinate.
Algebraically, equation for calculating the addition operation is:
P=(X1,Y1) (3)
Q=(X2,Y2) (4)
R=(P+Q)=(X3,Y3) (5)
First, define a line that connect P and Q. This line will cross the elliptic curve on -R based on equation:
Y=aX+b (6)
a=(Y2-Y1)/(X2-X1) (7)
b=Y1-aX1 (8)
Substitute (6) into (2) yields:
X^3-(aX+b)^2+a+b=0 (9)
From three order polynomial equation and substitution a from (7) yields:
X3=(((Y2-Y1)/(X2-X1)^2)-X1-X2) (10)
Using line equation (6),(7),(8) and reflection equation yields:
Y3=-Y1+(((Y2-Y1)/(X2-X1))(X1-X3)) (11)
If P=Q so the addition above is called doubling operation.
For computation of doubling
product, a tangential line should be defined, that cross P point. This
tangential line will cross the elliptic curve in –R. For determining the
gradient, equation (2) is differentiated that yields:
a=(3X^2+a)/2Y
(12)
With the same way we can get:
X1=((3X1^2+a)/2Y1)^2-X1-X2 (13)
Y3=-Y1+((3X1^2+a)(X1-X3)/2Y1) (14)
The scalar product (Q=kP) can be done using addition and doubling operation. The value knkn-1...k2k1k0 shifted one by one to the left from kn to k0. kn must be started by bit 1. If the shifted bit is 1 so the doubling operation done, and if the shifted bit is 0 the addition operation will be done.
This process continue until all of the bit on k shifted and the total computation calculated.
Previously, we must determine shape, reference point and the order of the elliptic curve then the cryptography process can be done. The shape of curve can be determined in three ways. The first is random method. The second is doned by firstly determined the orde of the curve (n) according to Hasse theorem:
p+1-2(p)^1/2 <= n<= p+1+2(p)^1/2 (15)
With p is prime value or 2^m value. The third method is done by Weil theorem.
This kind of cryptography can be used for giving better information security about the privacy of the messages, authentification of the sender and the information, authentification of the sender’signature and the change of the keys.
This algorithm offer faster computational time and lower complexity architecture compare with others. This computational resources can be used to implement elliptic curves cryptosystem’s scheme. Future work we will implement our architecture on CMOS technology using VLSI design methodology to obtain practical implementation of finite arithmetic chip ( IC ). This IC can be used to implement elliptic curves cryptosystem.
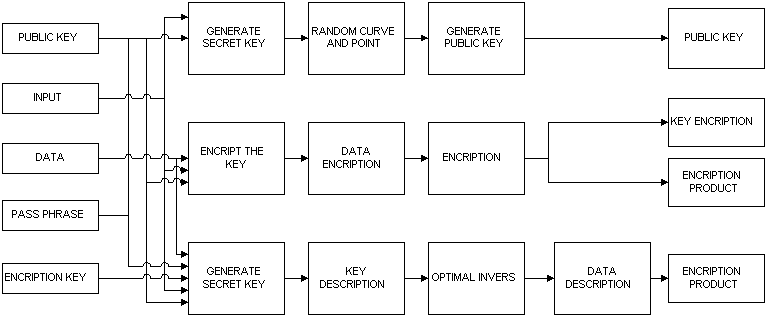
The block diagram of the system is shown in the drawing below:

.